Команда специалистов по математическому моделированию из РУДН предложила качественную модель эволюции вируса и появления новых штаммов. Результаты исследования могут сделать прогнозирование поведения вирусов более эффективным и помочь в разработке новых противовирусных препаратов. Статья опубликована в журнале Mathematics.
Взаимодействие вируса с организмом человека — очень сложное явление, которое можно свести к двум процессам: вирус размножается в клетках-хозяевах, и организм противостоит инфекции посредством иммунного ответа. Более пристальный взгляд на вирусную инфекцию показывает, что вирусы конкурируют за клетки-хозяев, изменяются под воздействием противовирусных препаратов и мутируют во время своей репликации. Они могут развиваться с очень высокой скоростью за счет модификации старых или приобретения новых последовательностей РНК или ДНК. Из-за этих и многих других факторов биологам сложно предсказать динамику эволюции вируса, предвидеть появление новых штаммов и оценить их потенциальные уровни устойчивости.
Команда Виталия Вольперта, математика из РУДН, предложила математическую модель, описывающую эволюцию и диверсификацию квазивидов вирусов. Модель показывает динамическое взаимодействие между репликацией, мутацией и элиминацией вируса. Результаты работы могут быть использованы для прогнозирования появления штаммов вирусов, способных избегать иммунного распознавания и сопротивляться противовирусным препаратам.
Чтобы не усложнять, модель показывает нам, что существующие штаммы развиваются, чтобы уменьшить конкуренцию между вирусами, ослабить выведение вируса за счет иммунного ответа и стать менее чувствительным к лекарствам. Эта тенденция приводит к появлению устойчивых к лекарствам штаммов/
Виталиq Вольперт, математик из РУДН
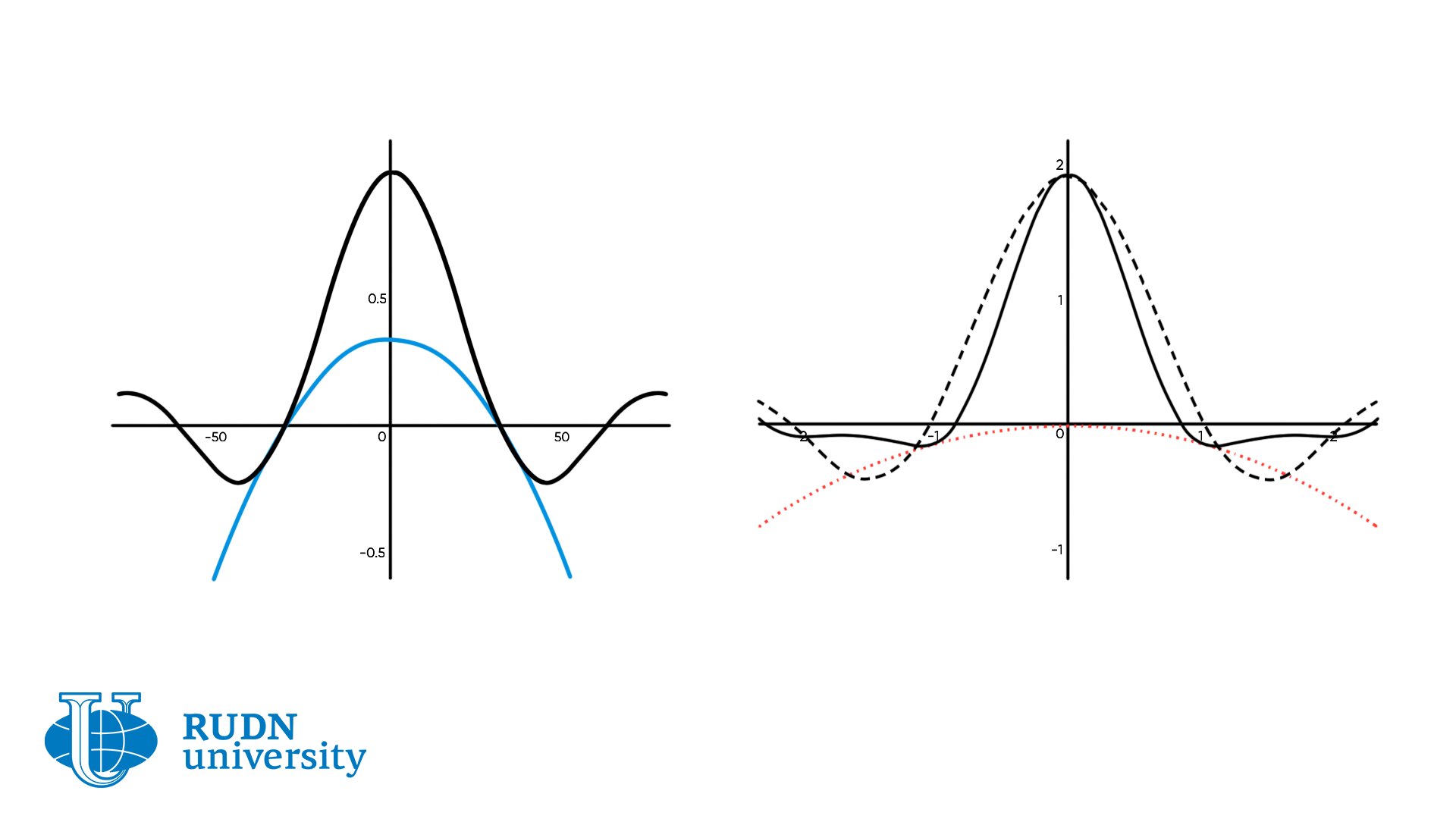
Работая вместе со своими коллегами, ученый описал штамм вируса как локализованный раствор, сосредоточенный вокруг данного генотипа. Возникновение новых штаммов соответствует периодической волне, распространяющейся в пространстве генотипов. Возникновение новых пиков распространения в процессе распространения волн совпадает с появлением новых штаммов вирусов. Команда описала условия возникновения периодических бегущих волн и их динамику, проанализировав устойчивость пространственно однородных стационарных решений.
Модель представлена нелокальным уравнением реакции-диффузии для плотности вируса. Уравнение имеет два интегральных члена, которые соответствуют нелокальным эффектам взаимодействия вируса с клетками-хозяевами и иммунными клетками.
Новая модель качественна и применима к различным вирусным инфекциям. Однако, чтобы лучше описать динамику квазивидов вирусов, необходимо знать их индивидуальные особенности, такие как характер их мутаций, взаимодействие с иммунной системой и ответ на противовирусные препараты.
«Используя нашу модель, можно разработать различные методы предотвращения распространения вирусных инфекций по тканям организма и появления новых штаммов , то есть распространения в пространстве генотипов. Однако для того, чтобы эти подходы имели практическую реализацию, они должны быть в сочетании с экспериментальными и клиническими данными», — объясняет Виталий Вольперт.
Модель имеет ряд ограничений, поскольку основана на нескольких упрощениях. А именно, она не принимает во внимание существование множества иммунных клеток и цитокинов (небольших информативных пептидных молекул), которые принимают участие в иммунном ответе, или сложных процессах внутриклеточной регуляции и репликации вируса. Однако эти ограничения помогают ученым определить некоторые общие эволюционные особенности квазивидов вирусов, которые было бы трудно идентифицировать в более сложной модели. Работа команды ученых может быть использована как основа для дальнейших расследований.
Читать также
Ледник «Судного дня» оказался опаснее, чем думали ученые. Рассказываем главное
Появилось сразу два доказательства внеземной жизни. Одно на Венере, другое — неизвестно где