От радуг, речных изгибов и теней до паутины, сот и отметин на шкурах животных — видимый мир полон закономерностей, которые можно описать математически. Рассказываем о самых интересных из них.
Математика в природе
Первые древнегреческие философы пытались описать и объяснить порядок в природе, предугадывая современные идеи. В своих работах о закономерностях природы Платон (около 427–347 до н. э.) писал о существовании универсалий. Он предполагал, что они состоят из идеальных форм (др.-греч. εἶδος, форма), а физические объекты — это не более чем несовершенные копии. Таким образом, цветок может быть примерно круглым, но это никогда не будет идеальный круг. Пифагор рассматривал закономерности в природе, так же, как и гармонии в музыке, берущими начало из числа, как первоначала всего сущего. Эмпедокл в какой-то степени предвосхитил эволюционное объяснение структуры организмов Дарвина.
В 1202 году Леонардо Фибоначчи открыл последовательность чисел Фибоначчи западному миру в своей «Книге абака». Фибоначчи привел (несуществующий) биологический пример численного роста теоретической популяции кроликов. В 1917 году Дарси Томпсон (1860–1948) опубликовал свою книгу «О росте и форме». Его описание взаимосвязи филлотаксиса (расположения листьев на стебле растения) и чисел Фибоначчи (математическое отношение закономерностей спирального роста в растениях) стало классическим. Он показал, что простые уравнения могут описать все с виду сложные закономерности спирального роста рогов животных и раковин моллюсков.
Тюринг, Плато, Геккель, Цейзинг — знаменитые деятели искусства и науки — искали строгие законы математики и находили ее в красоте природы.
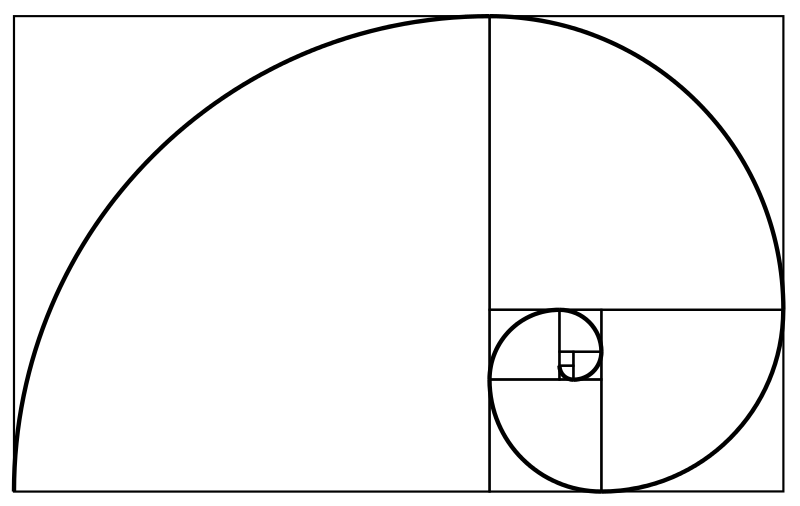
Спираль Фибоначчи — геометрическая прогрессия красоты
Спирали распространены среди растений и некоторых животных, особенно среди моллюсков. Например, у моллюсков-наутилид каждая ячейка их раковины — примерная копия следующей, масштабированная константой и выложенная в логарифмическую спираль.

Чаще всего в природе встречается последовательность Фибоначчи. Она начинается с чисел 1 и 1, а затем каждое последующее число получается путем сложения двух предыдущих чисел. Следовательно, после 1 и 1 следующее число — 2 (1 + 1). Следующее число — 3 (1 + 2), затем 5 (2 + 3) и так далее.
Спирали в растениях наблюдаются в расположении листьев на стебле, а также в структуре бутона и семян цветка — например, у подсолнуха или структуры плода ананаса и салака. Последовательность Фибоначчи можно заметить и у сосновой шишки, где огромное количество спиралей расположено по часовой и против часовой стрелки. Эти механизмы объясняются по-разному — математикой, физикой, химией, биологией. Каждое из объяснений верно само по себе, но необходимо учитывать их все.

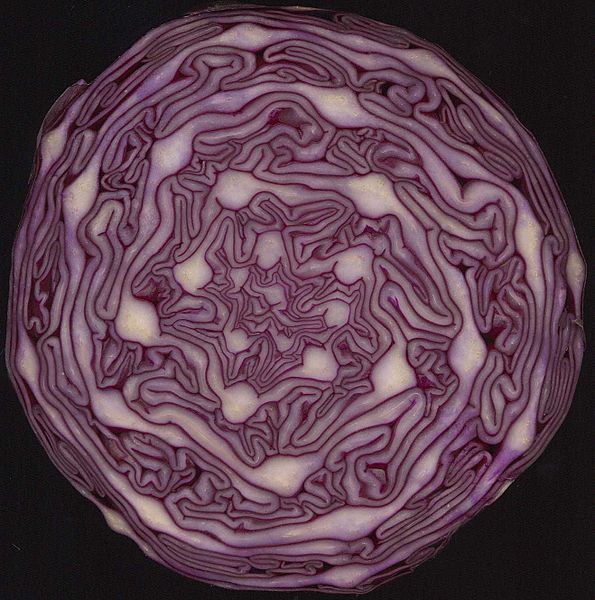


С точки зрения физики, спирали — конфигураций низких энергий, которые возникают спонтанно путем самоорганизации процессов в динамических системах. С точки зрения химии, спираль может быть образована реакционно-диффузионным процессом с привлечением как активации, так и ингибирования. Филлотаксис контролируется протеинами, которые управляют концентрацией растительного гормона ауксина, который активирует рост среднего стебля наряду с другими механизмами контроля относительного угла расположения бутона к стеблю. С точки зрения биологии листья расположены настолько далеко друг от друга, насколько позволяет естественный отбор, так как он максимизирует доступ к ресурсам, особенно к солнечному свету, для фотосинтеза.
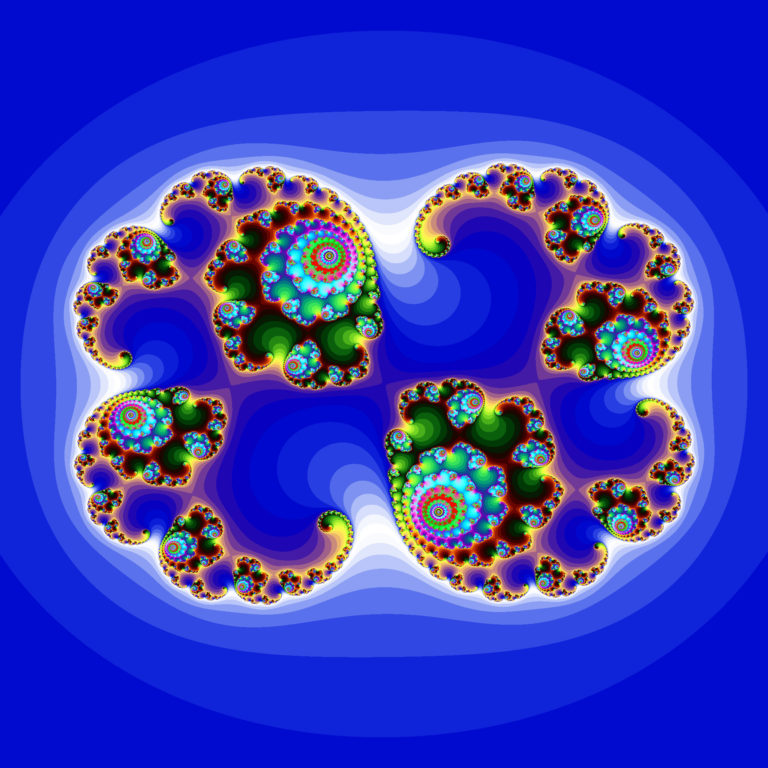
Фракталы — бесконечное (почти) повторение
Фракталы — еще одна интересная математическая форма, которую каждый видели в природе. Сам Фрактал — это самоподобная повторяющаяся форма, что означает, что одна и та же основная форма появляется снова и снова. Другими словами, если вы увеличите или уменьшите масштаб, везде будет видна одна и та же.
Эти самоподобные циклические математические конструкции, обладающие фрактальной размерностью, встречаются довольно часто, особенно среди растений. Самый известный пример — папоротник.

Кстати, бесконечная повторяемость невозможна в природе, поэтому все фрактальные закономерности — это только аппроксимации (приближения). Например, листья папоротников и некоторых зонтичных растений (например, тмин) являются самоподобными до второго, третьего или четвертого уровня.
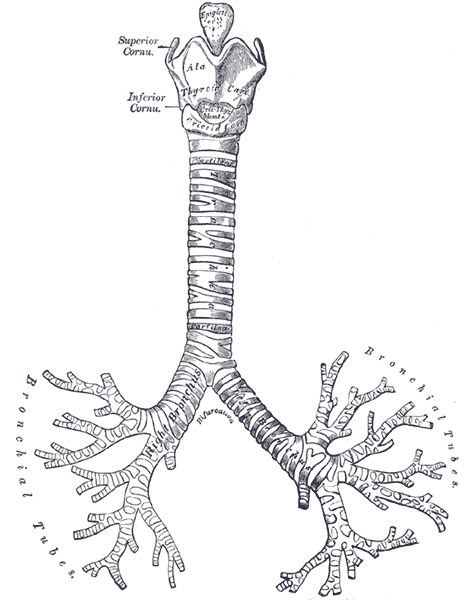
Схожие с папоротником паттерны встречаются также у многих растений (брокколи, капуста сорта Романеско, кроны деревьев и листья растений, плод ананаса), животных (мшанки, кораллы, гидроидные, морские звезды, морские ежи). Также фрактальные паттерны имеют место в структуре разветвления кровеносных сосудов и бронхов животных и человека.




Первые примеры самоподобных множеств с необычными свойствами появились в XIX веке в результате изучения непрерывных недифференцируемых функций (например, функция Больцано, функция Вейерштрасса, множество Кантора). Термин «фрактал» введен Бенуа Мандельбротом в 1975 году и получил широкую известность с выходом в 1977 году его книги «Фрактальная геометрия природы».

Особую популярность фракталы обрели с развитием компьютерных технологий, позволивших эффектно визуализировать эти структуры.
Многоугольники — инженерный гений
При достаточной наблюдательности в живой природе легко обнаружить строгую геометрию. В особом почете оказываются гексагоны — правильные шестиугольники.
Например, соты, в которых пчелы хранят золотистый нектар, — это чудеса инженерного искусства, набор ячеек в форме призмы с правильным шестиугольником в основании. Толщина восковых стенок строго определена, ячейки немного отклоняются от горизонтали, чтобы вязкий мед не вытекал, и соты находятся в равновесии с учетом влияния магнитного поля Земли. А ведь эту конструкцию без чертежей и прогнозов строят множество пчел, которые одновременно работают и как-то координируют свои попытки сделать соты одинаковыми.

Если вы подуете на пузырьки на поверхности воды, чтобы согнать их вместе, то они приобретут форму шестиугольников — или, по крайней мере, приблизятся к ней. Вы никогда не увидите скопище квадратных пузырей: если даже четыре стенки соприкоснутся, они немедленно перестроятся в конструкцию с тремя сторонами, между которыми будут примерно равные углы в 120 градусов. Почему так происходит?

Пена — это множество пузырей. В природе существуют пенопласты из разных материалов. Пена, состоящая из мыльных пленок, подчиняется законам Плато, согласно которым три мыльные пленки соединяются под углом 120 градусов, а четыре грани соединяются в каждой вершине тетраэдра под углом 109,5 градусов. Затем по законам Плато требуется, чтобы пленки были гладкими и непрерывными, а также имели постоянную среднюю кривизну в каждой точке. Например, пленка может оставаться почти плоской в среднем, имея кривизну в одном направлении (например, слева направо), и в то же время искривляться в обратном направлении (например сверху вниз). Лорд Кельвин сформулировал задачу упаковки клеток одного объема наиболее эффективным способом в виде пены в 1887 году; его решение — кубическая сота со слабо изогнутыми гранями, удовлетворяющими законам плато. До 1993 года это решение оставалось лучшим, пока Денис Ваэрен и Роберт Фэлан не предложили структуру Ваэра-Фэлена. Впоследствии эта структура была адаптирована для внешней стены Пекинского национального плавательного комплекса, построенного для проведения летних Олимпийских игр 2008 года.

Природа озабочена экономией. Пузыри и мыльная пленка состоят из воды (и слоя мыльных молекул), и поверхностное натяжение сжимает поверхность жидкости таким образом, чтобы она занимала наименьшую площадь. Поэтому капли дождя при падении принимают форму, близкую к сферической: у сферы наименьшая площадь поверхности по сравнению с другими фигурами того же объема. На восковом листке капли воды сжимаются в маленькие бусинки по той же причине.
Поверхностное натяжение объясняет и тот узор, который образуют пузыри или пена. Пена стремится к такой конструкции, при которой общее поверхностное натяжение будет минимальным, а значит, минимальной должна быть и площадь мыльной мембраны. Но конфигурация стенок пузырей должна быть прочной и с точки зрения механики: натяжение в разных направлениях на «перекрестке» должно быть идеально сбалансировано (по тому же принципу нужен баланс при строительстве стен собора). Трехстороннее соединение в пленке из пузырьков и четырехстороннее — в пене — комбинации, которые достигают этого баланса.
Читать далее
Создана первая точная карта мира. Что не так со всеми остальными?
В НАСА рассказали, как они доставят образцы Марса на Землю
Уран получил статус самой странной планеты в Солнечной системе. Почему?